CTの原理

CT＆その他の知識⑤

簡易説明

通常のレントゲンでは、2次元・平面での撮影しか出来ません。

ＣＴ(Computed tomography)では、体の周りを回って撮影し、断層撮影が可能となり、それらのデータをコンピューター処理することにより、パソコンでの立体画像を見る事が出来ました。

専門的視野での解説

立体画像をみせてくれるCT
今回はCTが３次元のデータをどうやって撮影しているのかについてお話します。

↓医科用CTスキャン

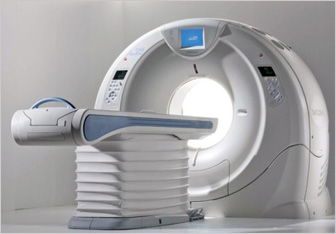
CTスキャンの原理
CTではX線源から人体に向けて照射されたX線は人体内部を通過し一部吸収されて減衰した後、反対側の検出器で受けます。

人体内部の各位置でのX線吸収率の違いにより、検出値の分布（下図中央の図）が変化します。
そして、X線源と検出器の組を少しずつ回転させて撮影を繰り返します。
このようにして得られた情報をコンピュータ処理することによって、対象物中のそれぞれの位置でのX線の吸収量を、黒から白に至る輝度（明るさ）として表示したものがＣＴ画像です。

CT画像では、骨の部分などはX線の吸収が大きいので白く見え、空気など吸収が少ない部分は黒く見えます。
また、これらの中間の吸収を示す部分（水や筋肉など）は灰色に見えます。

CTスキャンの数学的な原理は以下のとおりです。

人体の画像（減衰率分布）を f(x, y) とし、
ある角度θでの検出値の分布（X軸への投影データ）を R(θ, X)とすると、
R(θ, X) = ∫-∞∞ f(x, y) dY
となります。

ここで、X-Y はｘｙ座標系をθだけ回転させた座標系です。
X = xcosθ + ysinθ
Y = -xsinθ + ycosθ

R(θ, X)を f(x, y) のラドン（Radon）変換と呼びます。

色々な角度θに対するR(θ, X)から f(x, y)を求めることができれば、人体の画像（断層写真）が得られることになります。
このために、以下のようにフーリエ変換を利用します。

R(θ, X)をフーリエ変換したものをG(θ, r)すると、
（dXdY = dxdy）
G(θ, r) = ∫-∞∞ R(θ, X)e -jrX dX
= ∫-∞∞ ｛∫-∞∞ f(x, y) dY ｝e -jrX dX
= ∫-∞∞∫-∞∞ f(x, y) e -jr(xcosθ + ysinθ) dxdy
= F (rcosθ, rsinθ)

ここで、F(u, v) は f(x, y) の２次元フーリエ変換：
F(u, v) = ∫-∞∞∫-∞∞ f (x, y)e-j (ux + vy) dxdy
であり、任意の方向θへの投影データR(θ, X)のフーリエ変換G(θ, r)は、同じ方向に沿ったF(u, v)の値に等しくなることがわかります。

従って、色々な方向のG(θ, r)からF(u, v)の全体が得られ、これを２次元フーリエ逆変換すれば f(x, y) が求められることになります。

f (x, y) = 1/(4π2)∫-∞∞∫-∞∞ F(u, v)e j (ux + vy) dudv

ここで、極座標： u = rcosθ, v = rsinθを導入すると、（dxdy = rdrdθ）
f (x, y) = 1/(4π2)∫02π∫0∞ F (rcosθ, rsinθ)e jr(xcosθ + ysinθ) rdrdθ
= 1/(4π2)∫02π∫0∞ G(θ, r)e jr(xcosθ + ysinθ) rdrdθ
= 1/(4π2)∫02π｛∫0∞ G(θ, r) r e jr(xcosθ + ysinθ) dr ｝dθ

この式は、投影データ（ラドン変換）R(θ, X)のフーリエ変換 G(θ, r)に r を掛けたものをフーリエ逆変換し、それをあらゆる角度θについて求めて積分すれば（平均値を取れば）元画像 f(x, y) が得られることを示しています。

非常に難しい話でしたね。